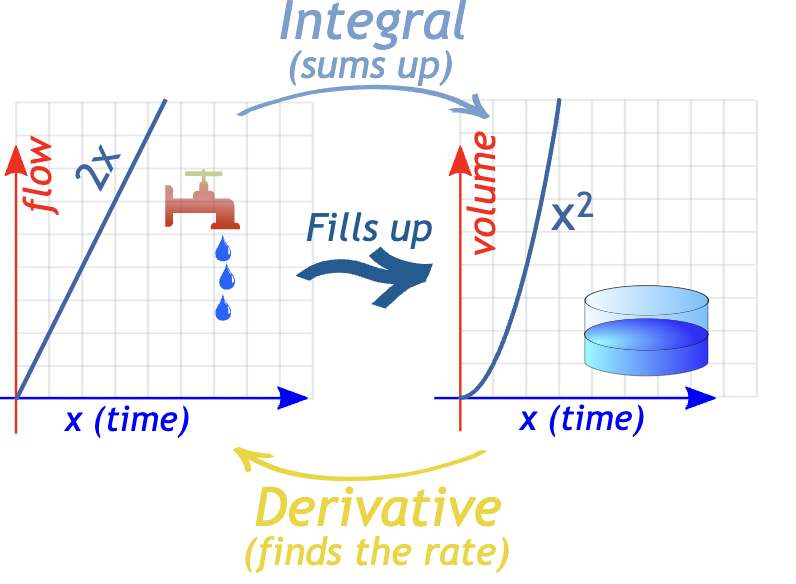
The term integrals refer to a collection or accumulation in things. Following the same idea, integrals become an important concept in mathematics. The concept corresponds to the summing of infinitesimal parts to find the content of a whole area or region. An integral is used in calculus as a mathematical function that can be interpreted as an area. Integrals are one of the fundamental objects of calculus in mathematics. It is a reverse process of differentiation or derivative of a function.
In mathematics, integral describes any displacement, area, volume, and other concepts that can be found by combining small parts of data. Integrals serve as a useful tool for solving problems involving the area of an arbitrary shape, the length of a curve, the volume of a solid, etc. Integral refers to the area of a region under a curve of any shape. The actual value of an area can be approximated by making small rectangular areas between the curve and the x-axis and then adding or integrating those areas. An integral of a function represents the area of a region by breaking it up into thin vertical areas and then adding up the areas between the lower and the upper limits. An integral of a function is defined by specifying it over an interval.
Integral is denoted by a numerical value that refers to the area under the curve enclosed by some interval. The integral of a function of ‘p’ will be the sum of the rectangles formed by the curve of that function at each interval of change in ‘p’. Integral is used for solving two types of problems as follows:
- Finding a function when its derivative is given.
- Finding the area enclosed by the graph of a function.
The integral is also called the anti-derivative because integration is the reverse process of differentiation. Integrals are considered to be a very effective tool in representing the area under graphs, the area bounded by a curve and a line, the area between two curves in a two-dimensional plane. Integrals can be used to calculate the volume of three-dimensional solids. It has also found its application in physics for the computation of displacement and motion problems.
What Are Integral Formulas?
In mathematics, the process of finding an integral is called integration. The integral of some function for some variable x refers to the area between the x-axis and the curve formed by the function. The process of finding integrals is called integration which is a fundamental and essential operation of calculus.
Integration formulas are derived considering the requirements of integration that apply to algebraic and trigonometric expressions, logarithmic, and exponential functions. In some cases, the integration formula is used for the integration of functions that results in the original functions for which the derivatives were given. These integration formulas are used to work in the reverse way of differentiation or as anti-derivative of a function to get the original function by integration. Suppose we have differentiated a function ‘f’ in an interval ‘i’ to get a group of functions in the said interval. If the values of all the functions in the interval ‘i’ are known, then we can determine the function ‘f’ using the integration formula.
There are different types of integration methods. Each method involves the application of a specific formula in finding the integrals. These are as follows:
- Integration by parts formula: When a given function is expressed as a product of two functions, this formula is applied to evaluate the integral.
- Integration by substitution formula: When a function is expressed as a function of another function, this formula is applied.
- Integration by partial fractions formula: This formula is used when we need to find the integral of a function P(x)/Q(x) which is an improper fraction.